CONVOLUTION
CONVOLUTION
CONVOLUTION
CONVOLUTION
Le produit de convolution de signaux discrets étant noté * :CONVOLUTION
Le produit de convolution de signaux discrets étant noté * :CONVOLUTION
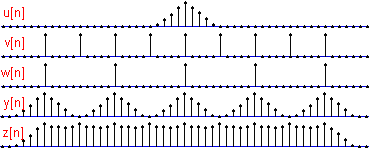
CONVOLUTION

CONVOLUTION
ECHANTILLONNAGE
ECHANTILLONNAGE
ECHANTILLONNAGE
Soit fmax la composante fréquentielle la plus élevée d'un signal et fech la fréquence d'échantillonnageECHANTILLONNAGE
ECHANTILLONNAGE
ECHANTILLONNAGE
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
La TFD des N échantillons temporels en consiste en un calcul des N échantillons fréquentiels Ek au moyen de:TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
La transformée de Fourier d'un signal en discret et apériodique a pour formule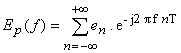
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
figure 1
figure 2TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
figure 1
figure 2TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
figure 1
figure 2TRANSFORMEE DE FOURIER ET DUALITE TEMPS FREQUENCE
figure 1
figure 2RECONSTITUTION
On peut reconstituer un signal analogique à partir de ses échantillonsFENETRES
Un signal temporel périodique se décompose en séries de Fourier. La limitation de cette décomposition un nombre fini de termes harmoniquesFENETRES
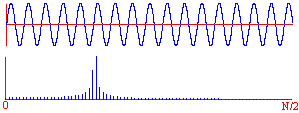
Voici N échantillons d'un signal parfaitement sinusoïdal, représenté avant fenêtrage.
Après avoir subi une multiplication par une fenêtre, le spectre de ce signal est calculé au moyen d'une TFD.
Le résultat, représenté sur une demi période fréquentielle, permet de penser que cette fenêtre était:FENETRES
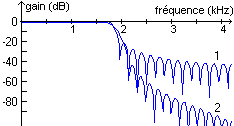
Voici les réponses en fréquence de deux filtres RIF passe-bas d'ordre 51, calculés par la méthode du fenêtrage pour 2 fenêtres différentes. Au vu de ces courbes, on peut affirmer queTRANSFORMEE EN Z
TRANSFORMEE EN Z
TRANSFORMEE EN Z
TRANSFORMEE EN Z
TRANSFORMEE EN Z
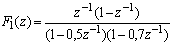
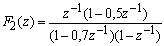
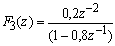
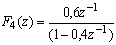
TRANSFORMEE EN Z
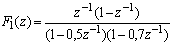
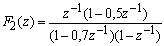
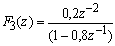
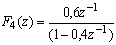
TRANSFORMEE EN Z
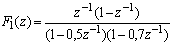
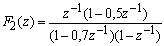
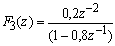
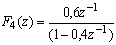
TRANSFORMEE EN Z
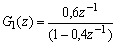
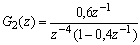
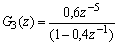
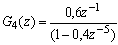
TRANSFORMEE EN Z
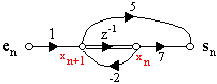
Ce graphe a pour fonction de transfertTRANSFORMEE EN Z
Cette réponse impulsionnelle est celleTRANSFORMEE EN Z
Le filtre, dont voici la réponse impulsionnelle, a ses pôles enTRANSFORMEE EN Z
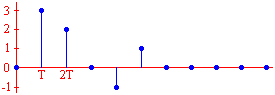
Le filtre, dont voici la réponse impulsionnelle, a pour fonction de transfertTRANSFORMEE EN Z
Soit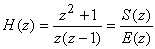 la fonction de transfert d'un filtre numérique
la fonction de transfert d'un filtre numériqueTRANSFORMEE EN Z
Dans le plan z,TRANSFORMEE EN Z
Un signal d'équation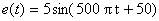 est échantillonné à 1000 Hz. Les échantillons e(kT) issus de cet
échantillonnage sont traités numériquement par un filtre de fonction de
transfert
est échantillonné à 1000 Hz. Les échantillons e(kT) issus de cet
échantillonnage sont traités numériquement par un filtre de fonction de
transfert 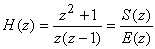 . Il en résulte des échantillons de sortie s(kT)
. Il en résulte des échantillons de sortie s(kT)FILTRAGE
FILTRAGE
FILTRAGE
La réponse fréquentielle de ce filtre numériqueFILTRAGE
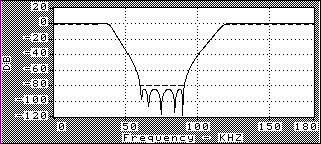
Le filtre caractérisé par cette courbe de réponse en fréquenceFILTRAGE
FILTRAGE
Le filtre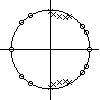 , caractérisé par ses pôles (x) et zéros (o) dans le plan z,
, caractérisé par ses pôles (x) et zéros (o) dans le plan z,FILTRAGE
Le filtre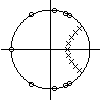 , caractérisé par ses pôles (x) et zéros (o) dans le plan z,
, caractérisé par ses pôles (x) et zéros (o) dans le plan z,FILTRAGE
Le filtre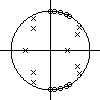 , caractérisé par ses pôles (x) et zéros (o) dans le plan z,
, caractérisé par ses pôles (x) et zéros (o) dans le plan z,FILTRAGE
Le filtre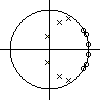 , caractérisé par ses pôles (x) et zéros (o) dans le plan z,
, caractérisé par ses pôles (x) et zéros (o) dans le plan z,FILTRAGE
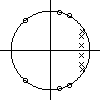
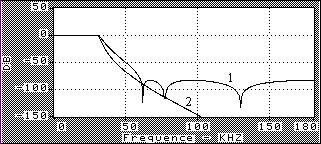
Le filtre caractérisé par ses pôles (x) et zéros (o) dans le plan z est, au vu de ses pôles et zéros, celui qui a la courbe de réponse en fréquence